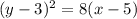Question

A parabola drawn on a coordinate plane has vertex (5,3) and focus (7,3) What is the value of a when the equation of the parabola is expressed in the form (y - k) = a (z - h)?

Answer 1

The equation of the parabola is;

`(y-3)^2=8(x-5)`

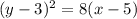
Step-by-step explanation:

Given the vertex;

`(h,k)=(5,3)`

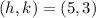
and focus;

`(h+a,k)=(7,3)`

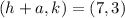
From the coordinates of the focus and the vertex we can observe that the focus and the vertex are on the same y-cordinates which means that they are on the same horizontal line.

So, the line of symmetry is perpendicular to the y axis and the parabola is an horizontal parabola.

The equation of the horizontal parabola can be derived using the equation;

`(y-k)^2=4a(x-h)`

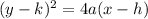
Given;

`\begin{gathered} h=5 \\ k=3 \\ h+a=7 \\ a=7-h=7-5 \\ a=2 \end{gathered}`

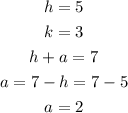
Substituting the values;

`\begin{gathered} (y-k)^2=4a(x-h) \\ (y-3)^2=4(2)(x-5) \\ (y-3)^2=8(x-5) \end{gathered}`

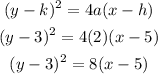
Therefore, the equation of the parabola is;

`(y-3)^2=8(x-5)`