Question

Which steps transform the graph of y = x^2 to y = -(x-3)^2 + 2?a) translate 3 units to the right; translate up 2 unitsb) reflect across the x-axis; translate 3 units to the left; translate down 2 unitsc) translate 3 units to the left; translate down 2 unitsd) reflect across the x-axis; translate 3 units to the right; translate up 2 units

Answer 1

We have to find the transformations to transform x² to -(x-3)² + 2.

We have a reflection over the x-axis, as we have a negative sign for the term (x-3)².

As we have a 3 inside the quadratic term, we have a translation on the x-axis.

Also, the independent term correspond to a translation in the y-axis.

We then can start then with a reflection across the x-axis.

The transformation is:

`x^2\longrightarrow-x^2`

Then, we can translate it 3 units to the right and the transformation becomes:

`-x^2\longrightarrow-(x-3)^2`

Finally, there is a translation in the vertical axis of 2 units:

`-(x-3)^2\longrightarrow-(x-3)^2+2`

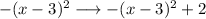
Answer: Reflect over the x-axis, translate 3 units to the right, translate up 2 units. [Fourth option]