Given
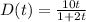
To find how much waste will the pumping station deliver during the 8 hour period.
Step-by-step explanation:
It is given that,
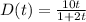
Then for t=1,
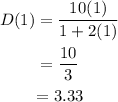
For t=2,
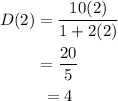
For t=3,
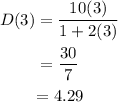
For t=4,
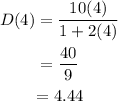
For t=5,
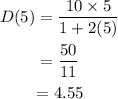
For t=6,
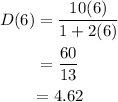
For t=7,
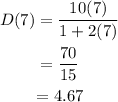
For t=8,
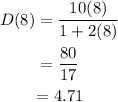
Then,
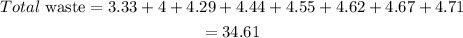
Hence, the total waste delivered is 34.61.