The Solution:
Given:
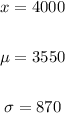
Applying the Z-statistic formula:
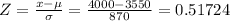
From the Z-scores tables:
The approximate probability of having a car weight that is more than 4000 pounds is:
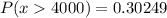
Converting the above probability to percent, we have:
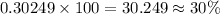
Therefore, the correct answer is [ option D ]