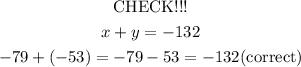Question

The sum of two numbers is -132. If twice the smaller number is one more than three times the largernumber, what are the two numbers?

Answer 1

Let the smaller number =x

Let the larger number = y

The first sentence states that the sum of the numbers is -132

`x+y=-132\ldots\ldots\ldots\ldots\ldots..(eqn\text{ 1)}`

The second sentence stated that twice the smaller number is one more than the larger number

`\begin{gathered} 2x-1=3y\ldots\ldots\ldots\ldots\ldots\text{.}(\text{eqn 2)} \\ \end{gathered}`

Solving simultaneously, let's make x the subject of the formula in Eqn 1

`x=(-132-y)\ldots\ldots\ldots\ldots\ldots(\text{eqn 3)}`

Substitute eqn 3 in eqn 2 we will have ,

`\begin{gathered} 2x-1=3y \\ 2(-132-y)-1=3y \\ -264-2y-1=3y \\ By\text{ collecting like terms we will have} \\ -264-1=3y+2y \\ 5y=-265 \\ \text{divide both sides by 5} \\ (5y)/(5)=-(265)/(5) \\ y=-53 \end{gathered}`

to find x substitute y=-53 in eqn 3

`\begin{gathered} x=-132-y \\ x=-132-(-53) \\ x=-132+53 \\ x=-79 \end{gathered}`

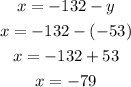
Therefore,

The numbers are -79 and -53

`\begin{gathered} \text{CHECK!!!} \\ x+y=-132 \\ -79+(-53)=-79-53=-132(\text{correct)} \end{gathered}`
`\begin{gathered} \text{CHECK!!!} \\ 2x-1=3y \\ 2(-79)-1=3(-53) \\ -158-1=-159 \\ -159=-159(\text{correct)} \end{gathered}`