Given a normal distribution with a mean of 100 and a standard deviation of 15:
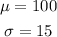
The graph of the Bell curve is:
a)
To find the percentage of the population with an IQ between 70 and 130, we need to find the z-scores, using the equation:
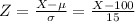
Then, the z-scores of 70 and 130 are:
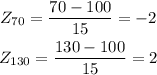
Then, the proportion can be calculated using the probability:
![P(-2Looking at z-distribution tables, this probability is (to two decimal places):[tex]P(-2<strong>Then, 95% of the population has an IQ between 70 and 130.</strong><p>b)</p><p>Unusually high scores are often calculated as those values above 3 standard deviations above the mean, so if in this case the mean is 100, and the standard deviation is 15, then the unusually high scores are:</p>[tex]\begin{gathered} \mu+3\sigma=100+3\cdot15=100+45=145 \\ \Rightarrow IQ\ge145 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/x2bu3733qru3u662j7vz.png)
c)
The range of IQ within 3 standard deviations is:
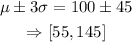
Then, the corresponding z-scores are:
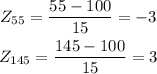
The proportion can be calculated using the probability:
[tex]P(-3Using a z-distribution table, this probability is (to 3 decimal places):[tex]P(-3
Then, 99.7% of the population will have an IQ score within 3 standard deviations of the average IQ score.