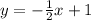Question

1. Create an equation of a straight line in slope-intercept form.2. Find a parallel and perpendicular line to your original equation.

Answer 1

The slope intercept form of a line equation is:

`y=mx+b`

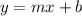
Where "m" is the slope and "b" is the y-intercept.

To create one line, we just need to choose values for "m" and "b", for example, let's pick m = 2 and b = 1.

Then the line is:

`y=2x+1`

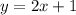
Every parallel line will have the same slope, so to find a different line that is paralle to it, we just need to maintain the same slope (the same "m") and change "b", for example, le'ts pick b = 2 now.

A parallel line is, then:

`y=2x+2`

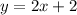
The slope of a perpendicular line can be found by inverting the slope and changin its sign, that is:

`m^(\prime)=-(1)/(m)`

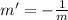
So, the slope of a line perpendicular to the original will be:

`m^(\prime)=-(1)/(2)`

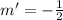
The "b" value can be any value and the line will still be perpencular. Le'ts pick b = 1 again.

So, a perpendicular line is:

`y=-(1)/(2)x+1`

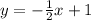
Original:

`y=2x+1`

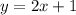
Parallel:

`y=2x+2`

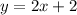
Perpendicular:

`y=-(1)/(2)x+1`