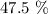In the question we are given that the mean of the data is 40 and the standard deviation is 6. We are now asked to find the approximate number of light bulb replacement between 40 and 52.
Step-by-step explanation
To begin with we will convert 40 and 52 to its rescpective z-scores.
![\begin{gathered} z=(x-\mu)/(\sigma) \\ x=\text{observed value} \\ \mu=\operatorname{mean} \\ \sigma=\text{standard deviation} \end{gathered}]()
For 40
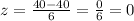
For 52
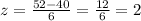
Now we will use the gaiven rule to figure out the percentage.
Explaining the 68-95-99.7 rule for a Normal Distribution. 68% of the data is within 1 standard deviation, 95% is within 2 standard deviation, 99.7% is within 3 standard deviations.
For 40 we got 0 and for 52 we got 2. This impies that the z -score of 0 gives a value thats around the mean while a z-score of 2 gives a value thats two standard deviation away from the mean.
Between the mean and two standard deviation of the mean, gives half of the 95%. Therfore we will have

Answer: