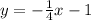Question

For each description, write the equation of the line in point-slope form and in slope-intercept form.The line passes through the two points (4,-2) and (-8,1)

Answer 1

The point-slope form is as follows:

`y-y_P=m(x-x_P)`

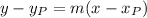
Where m is the slope and (xP, yP) is a point on the line. We can use any opint as long as it is on the line.

The slope-intercept form is:

`y=mx+b`

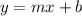
Where m is the same slope and b is the y-intercept. We can find it by either using the y-intercept or by solving the slope-point form for y.

First, we need to find the slope using the points (4, -2) and (-8, 1):

`m=(y_2-y_1)/(x_2-x_1)=(1-(-2))/(-8-4)=(1+2)/(-12)=(3)/(-12)=-(1)/(4)`

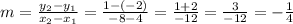
So, to find the point-slope form, we can use either points, so let's use (4, -2):

`\begin{gathered} y-(-2)=-(1)/(4)(x-4) \\ y+2=-(1)/(4)(x-4) \end{gathered}`

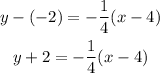
And to find the slope-intercept, we just solve the parenthesis and solve for y:

`\begin{gathered} y+2=-(1)/(4)(x-4) \\ y+2=-(1)/(4)x+1 \\ y=-(1)/(4)x+1-2 \\ y=-(1)/(4)x-1 \end{gathered}`

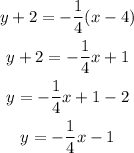
So, one of the possible point-slope forms is:

`y+2=-(1)/(4)(x-4)`

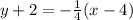
And the slope-intercept form is:

`y=-(1)/(4)x-1`