Question

I'm being asked to figure out whether or not the graphs are one to one functions, i already determined that this one is but im unsure of how to graph its inverse since the graph is my only bit of information

Answer 1

We need to graph the inverse function of the function we have in the image.

To do this, we can take the original graph of the function and identify some points as follows:

To convert a point of the original function, to a point of the inverse function, we use the following rule:

`(x,y)\longrightarrow\text{inverse function}\longrightarrow(y,x)`

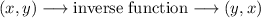
In the inverse function, the coordinates of the points are interchanged.

Thus we convert the points we have to points of the inverse function:

`\begin{gathered} (2,0)\longrightarrow\text{inverse function}\longrightarrow(0,2) \\ (0,-2)\longrightarrow\text{ inverse function}\longrightarrow(-2,0) \end{gathered}`

We will use the points (0,2) and (-2,0) as the base to draw the inverse function:

And since the inverse function is as if we took the original function and reflect it in a mirror, we can complete the graph by tracing a line that is just like the original but upside down.

The inverse function will look as follows: