Okay, here we have this:
Considering the provided function, we are going to calculate the inflection points, so we obtain the following:
Let's remember that the inflection points are those where the derivative is equal to zero or is undefined and changes sign, so let's calculate it:
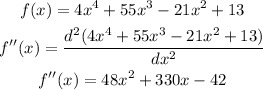
Now let's find the points where the second derivative is zero or undefined:
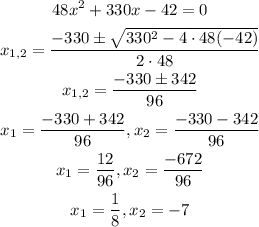
Now we will calculate the third derivative of the function and we will evaluate in these roots, if the result is different from zero then we have an inflection point:
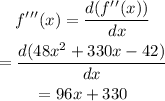
And evaluating in the two roots:
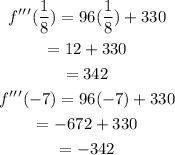
We observe that since the result is different from zero, then the two are inflection points, we substitute in the original function to find the y-coordinate of the points:
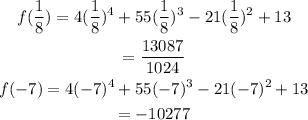
Finally we obtain that the inflection points are: (1/8, 13087/1024) and (-7, -10277).