Question

-8) let f(x) = - 2x^3 (x - 2)^2(x + 3). Do the following:a). Find the zeros and their multiplicity.b). What is the end behavior and the maximum number of turning points?c) graph f(x).

Answer 1

Given:

`f\mleft(x\mright)=-2x^3\left(x-2\right)^2\left(x+3\right)`

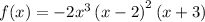
Required:

We need to find the zeros of the function, the end behavior, and the maximum number of turning points and draw the graph.

Step-by-step explanation:

a)

Set f(x)=0 to find the zeros of the given function.

`-2x^3(x-2)^2(x+3)=0`

`x^3(x-2)^2(x+3)=0`
`x^3=0,(x-2)^2=0,(x+3)=0`

`x=0,x-2=0,x+3=0`

`x=0,x=2,x=-3.`

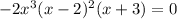
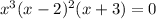
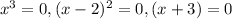
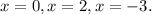
The zeros are 0,2 and -3.

Recall that The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity.

The multiplicity 0 is 3.

The multiplicity 2 is 2.

The multiplicity -3 is 1.

b)

The end behavior:

Taking the limit of negative infinity to the given function.

`\lim_(x\to-\infty)f(x)=\lim_(x\to-\infty)(-2x^3(x-2)^2(x+3))`

`\lim_(x\to-\infty)f(x)=-2(-\infty)^3(-\infty-2)^2(-\infty+3)`

`\lim_(x\to-\infty)f(x)=-(-\infty)(\infty)(-\infty)`

`\lim_(x\to-\infty)f(x)=-\infty`
`As\text{ }x\rightarrow-\infty\text{ then }f(x)\rightarrow-\infty`

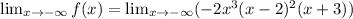
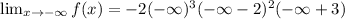
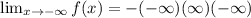
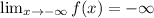
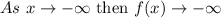
Taking the limit of infinity to the given function.

`\lim_(x\to\infty)f(x)=\lim_(x\to\infty)(-2x^3(x-2)^2(x+3))`

`\lim_(x\to-\infty)f(x)=-2(\infty)^3(\infty-2)^2(\infty+3)`

`\lim_(x\to-\infty)f(x)=-(\infty)(\infty)(\infty)`

`\lim_(x\to-\infty)f(x)=-\infty`

`As\text{ }x\rightarrow\infty\text{ then }f(x)\rightarrow-\infty`

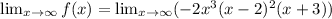
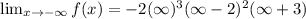
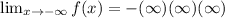
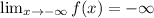
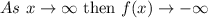
Recall that the maximum number of turning points of a polynomial function is always one less than the degree of the function.

The degree of the given function is 3+2+1=6.

The maximum number of turning points =6-1=5.

Final answer:

a)

Zeros of the function

`x=0,x=2,x=-3.`

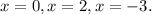
The multiplicity 0 is 3.

The multiplicity 2 is 2.

The multiplicity -3 is 1.

b)

End behavior:

`As\text{ }x\rightarrow-\infty\text{ then }f(x)\rightarrow-\infty`

`As\text{ }x\rightarrow\infty\text{ then }f(x)\rightarrow-\infty`

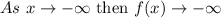
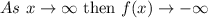
The maximum number of turning points is 5.

c)

The graph of the given function