Question

I need to find all three angles using law of cosines

Answer 1

Given the infromation about triangle ABC, we can use the law of cosines to find angles A and C:

`\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ \Rightarrow\cos A=(b^2+c^2-a^2)/(2bc) \\ \text{then:} \\ \cos A=((12)^2+(16)^2-(14)^2)/(2(12)(16))=(204)/(384) \\ \Rightarrow A=\cos ^(-1)((204)/(384))=57.9 \\ A=57.9 \end{gathered}`

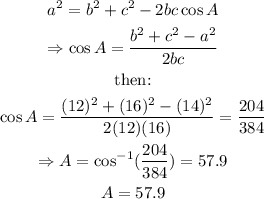
then, for angle C, we have:

`\begin{gathered} c^2=a^2+b^2-2ab\cos C \\ \Rightarrow\cos C=(a^2+b^2-c^2)/(2ab) \\ \Rightarrow\cos C=((14)^2+(12)^2-(16)^2)/(2(14)(12))=(84)/(336) \\ \Rightarrow C=\cos ^(-1)((84)/(336))=75.5 \\ C=75.5 \end{gathered}`

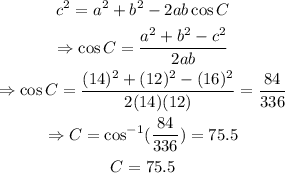
now, using the fact that the sum of interior triangles is 180, we have for angle B:

`\begin{gathered} 57.9+\measuredangle B+75.5=180 \\ \Rightarrow\measuredangle B=180-57.9-75.5=46.6 \\ \measuredangle B=46.6 \end{gathered}`

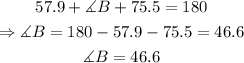
therefore, the measure of each angle is:

A=57.9

B=46.6

C=75.5