Given:
original population of the bacteria = 55 000
growth rate = 15% per hour
time = 5 hrs
The population after t hours can be calculated using the formula:
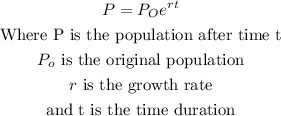
Substituting the given values into the formula, we have the population of the bacteria after 5 hrs to be:
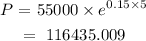
Hence, the population of the bacteria after 5 hours is 116435 bacteria