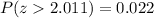In this question, we need to find a probability in the normal distribution. We have a population that is normally distributed. We can also see that this normal distribution has the same parameters as the standard normal distribution, that is, the mean is equal to 0°C and the standard deviation is equal to 1 (more precisely, 1.00°C).
In these questions, we need to use the z-scores (values for which we can consult the standard normal distribution values, a distribution that has the values for any normal distribution if we find the associated z-score). The z-score is given by:
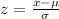
Where
• x is the raw value. The value for which we are finding the z-score.
,
• μ is the mean for the population.
,
• σ is the standard deviation for the population.
In this case, we only need to find the corresponding values for z = 2.011. We can consult a standard normal distribution table to find the corresponding values for the cumulative probability until z = 2.011, and then subtract this value from 1 to find the probability for which P(z > 2.011). We can also use technology (graphing calculators to find such a value).
Since z = 2.011, and we can check this as follows:
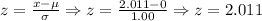
Then, if we find the cumulative probability for z = 2.011 in a standard normal distribution table (we can find this table in any Statistics book and on the internet too), that is, the cumulative probability from -∞ to the value z = 2.011. Then we have:
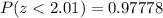
To find such a value (roughly speaking), we can proceed as follows:
1. At the left side column of the table, we will have values for z.
2. We need to find 2.0.
3. In the first file, above all the values for cumulative probabilities, we find other values for 2.00, 2.01, 2.02, and so on (they are described as 0.0, 0.01, 0.02, and so forth).
4. We got the value for which z = 2.0 and 0.01 ---> 0.97778 (other tables gives us 0.9778).
The consulted table only has values for z with two decimal places (z = 2.01). However, we can obtain an approximation to the actual value if we subtract this value from 1 (since we need the values for which z > 2.011). Then, we have:
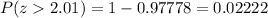
Then, the probability for P(z > 2.01) = 0.02222.
If we use technology (a graphing calculator), we can even find a more precise value, since we can use z = 2.011. We can use the cumulative probability in such a calculator, and then we need to subtract that value from 1 to find P(z>2.011) as we did before.
Using technology, we can see that the value for P(z>2.011) is 0.0221627283587. We can graph this probability as follows:
In summary, we can use the standard normal table to find a given probability for normally distributed data. However, we only have two decimal places when finding value for z. We can also use technology to find more precise values as z =2.011°C such this case. Then, we can say that:
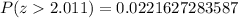
(If we are very precise).
If we round our value to three decimal places (thousandths) we have: