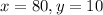Given the system of equations;

Also, some equivalent systems;
Step 1:

Step 2:

Step 3:

Statement Problem(a):
(i) What was done to the original system to get the system in step 1?
ANSWER:
Multiply equation 1 by 3.5 to produce equation3, and equation 2 is unchanged. We have;
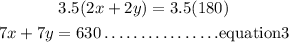
(ii) Explain why the system in step 1 shares the a solution with the original system.
ANSWER:
Systems of equations that have the same solution are called equivalent systems. They are equivalent systems because one of the equations is only transformed by multiplying 3.5 by it.
Statement Problem (b):
(i) What was done to the system in step 1 to get the system in step 2?
ANSWER:
Subtract equation 4 from equation 3 to produce equation 5 and equation 4 is unchanged. We have;
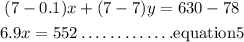
(ii) Explain why the system in step 2 shares the a solution with that in step 1.
ANSWER:
Systems of equations that have the same solution are called equivalent systems. They are equivalent systems because equation 5 is formed by subtracting equation 3 from equation 4.
Statement Problem (c):
What is the solution to the original system?
Solution:
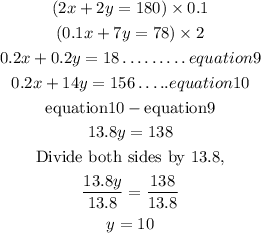
Then, we solve for x by substituting into equation9 9, we have;

Hence, the solution of the original system is;