Question

Let g (x) be the transformation of f (x)= IxI so that the vertex is at (-2, 5). Identify the rule for g (x) and its graph.

Answer 1

`g(x)=\lvert x+2\rvert+5`

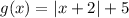
Step-by-step explanation

As the vertex is at (-2, 5), and the parent function is f(x)= IxI with a vertex in (0, 0), to get to (-2, 5) we have to move two units to the left of the horizontal axis and five units up of the vertical axis. The x represents the values in the horizontal axis, while y in the vertical, thus, to get those movements x and y would have to be:

`\begin{gathered} x=-2 \\ x+2=0 \end{gathered}`
`y=5`

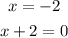
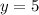
Then, applying these movements to our function we get:

`g(x)=\lvert{x+2}\rvert+5`

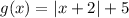
with the vertex in (–2, 5).