Question

Hello i am trying to help my 9th grade daughter who has autism do her test corrections. I have not taken Algebra 1 in over 20 yrs and am a little rusty. She gets easily frustrated and Im trying to do the leg work on it before going over it with her. Thanks for your assistance in advance

Answer 1

The two options marked are the correct ones.

When we have a function h(x) and add a constant k, the graph of the function is shifted up or down depending on the value of k (if it's positive shifts up and if it's negatives shifts down)

Since the asymptote is a vertical one, the shift on the verical axis will not change the asymptote, then we can rule out the option A.

The second option tell us to look the slope of the asymptote, but an asymptote is a point where the slope of the function is equal to infinity, adding a constant will only shift up and down , and will not result in a change of the slope. We can rule out option B

Now the options C and D must be true, but let's see why:

The x-intercept of a function is the point where the function "touches" the x-axis. We can find this points looking where the function is equal to 0. In this case, we have f(x) and g(x):

`\begin{gathered} f(x)=a^x \\ g(x)=a^x+k \end{gathered}`

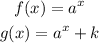
We can also write:

`g(x)=f(x)+k`

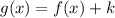
Now to find the x-intercept of f(x):

`f(x_0)=0`

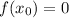
Where x0 is the x-coordinate of the x-intercept

Then we can replace in g(x):

`\begin{gathered} g(x_0)=0+k \\ g(x_0)=k \end{gathered}`

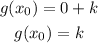
And that's how we can find the value of k using the x-intercept; thus B is correct

Now we can do the same for the y-intercept.

The y-intercept is the point where the function "touches" the y-axis. We can find this point by replacing x = 0.

Then:

`\begin{gathered} \begin{cases}f(x)=a^x \\ g(x)=a^x+k\end{cases} \\ then\colon \\ g\mleft(0\mright)=a^0+k \end{gathered}`

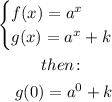
Any number to power 0 is equal to 1, then:

`g(0)=1+k`

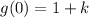
This way we can also find the value of k.