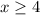Answer:
 or
or
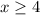
Explanation:
We are given that

We have to find the restricted domain of f which make the inverse of f.
Substitute x=4

One-to-one function:
The function is called one-to-one when
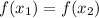 for
for
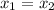
The function is one-to-one when
 or
or
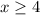
When the function is one-to-one then the function has inverse function.
If the function is not one-to-one then function has no inverse .
Therefore, the restricted domain of f which make the inverse of f(x) a function is given by
 or
or