Question

You have $ 10,000 dollars to buy fence to enclose a rectangular plot of land ( see figure at right). The fence for the top and bottom costs $4 per foot and for the sides it costs $3 per foot. Find the dimensions , x and y, of the plot with the largest area. For this largest plot, how much money was used for the top and bottom, x, and for the sides, y ?

Answer 1

Given:

The amount for buy fence = $ 10,000.

The cost for the top and bottom of the fence = $ 4 per foot.

The cost for the left ad right sides of the fence = $3 per foot.

The length of the top and bottom is x.

The length of the left and right is y.

Required:

We need to find the money that was used for the top and bottom, x, and for the sides, y.

Step-by-step explanation:

Consider the equation for the given model.

`4(2x)+3(2y)=10000`
`8x+6y=10000`

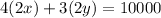
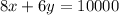
Isolate y, we get

`8x+6y-8x=10000-8x`
`6y=10000-8x`
`(6y)/(6)=(10000)/(6)-(8x)/(6)`
`y=(5000)/(3)-(4x)/(3)`

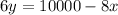
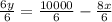
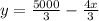
Multiply x and y, since the area of the given rectangle, is xy square feet.

`xy=(5000)/(3)x-(4x^2)/(3)`

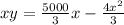
Let A =xy.

`A=(5000)/(3)x-(4x^2)/(3)`

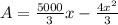
Differentiate the equation with respect to x.

`A^(\prime)=(5000)/(3)-(4(2x))/(3)`
`A^(\prime)=(5000)/(3)-(8x)/(3)`

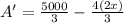
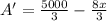
Equate this equation to zero.

`A^(\prime)=(5000)/(3)-(8x)/(3)=0`
`5000-8x=0`
`5000-8x+8x=0+8x`
`5000=8x`
`(5000)/(8)=(8x)/(8)`
`x=625\text{ feet.}`

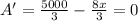
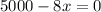
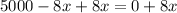
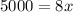
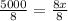
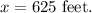
Substitute x =625 in the equation y.

`y=(5000)/(3)-(4(625))/(3)`
`y=(5000)/(3)-(2500)/(3)`
`y=(5000-2500)/(3)`
`y=(2500)/(3)`
`y=833.33`
`y=833.33feet`

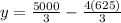
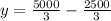
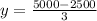
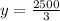
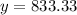
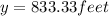
Replace x =625 in 8x to find the cost for the top and bottom.

`8*625=5000`

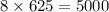
Replace y =833.33 in 6y to find the cost for the left and right sides.

`6*833.33=4999.98`
`=5000`
`A=xy=625*833.33=520831.25feet^2`

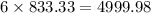
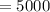
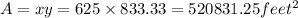
Final answer:

The area will be x times y or 520931.250square feet.

Top and bottom fencing will cost $5000, and sides will cost $5000.