Answer
The zeros of the polynomial function using the rational zero theorem is
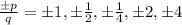
Step-by-step explanation
The given polynomial function is

What to find:
To find the zeros of the polynomial function the rational zero theorem.
Step-by-step solution:
The rational zero theorem: If a polynomial function, written in descending order of the exponents, has integer coefficients, then any rational zero must be of the form ± p/ q, where p is a factor of the constant term and q is a factor of the leading coefficient.
Considering the given polynomial function

The constant term, p = 4
The leading coefficient, q = 4
The factors of the constant p and the leading coefficient q are:
![\begin{gathered} p=\pm1,\pm2,\pm4 \\ \\ q=\operatorname{\pm}1,\operatorname{\pm}2,\operatorname{\pm}4 \end{gathered}]()
Hence, the zeros of the polynomial function using the rational zero theorem will be
![\begin{gathered} (\pm p)/(q)=(\pm1,\pm2,\pm4)/(\pm1,\pm2,\pm4) \\ \\ \frac{\operatorname{\pm}p}{q}=\operatorname{\pm}1,\operatorname{\pm}(1)/(2),\operatorname{\pm}(1)/(4),\operatorname{\pm}2,\operatorname{\pm}4 \end{gathered}]()