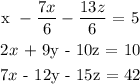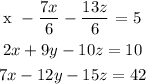
Step-by-step explanation:
6x - 7y - 13z = 30 ...equation 1
2x + 9y - 10z = 10 ...equation 2
7x - 12y - 15z = 42 ...equation 3
Multiply the 1st equation by 1/6:
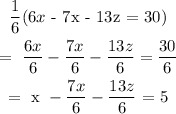
Since the multiplication is only applied to the 1st equation, the other equations will remain the same.
It becomes: