Question

Determine the axis of symmetry and the vertex of the given function. y = 2x2 − 12x + 21 Axis of symmetry: x = Vertex: ( , )

Answer 1

The vertex is (3,3) and the axis is 3

Answer 2

The vertex of the function is (h,k)=(3,3)

The axis of symmetry is x=3.

Explanation:

Given : Function
`y=2x^2-12x+21`

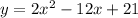
To find : Determine the axis of symmetry and the vertex of the given function.

Solution :

The quadratic function is in the form,
`y=ax^2+bx+c`

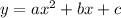
On comparing, a=2 , b=-12 and c=21

The vertex of the graph is denote by (h,k) and the formula to find the vertex is

For h, The x-coordinate of the vertex is given by,

`h=-(b)/(2a)`

`h=-(-12)/(2(2))`

`h=(12)/(4)`

`h=3`

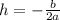
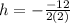
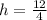
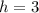
For k, The y-coordinate of the vertex is given by,

`k=f(h)`

`k=2h^2-12h+21`

`k=2(3)^2-12(3)+21`

`k=18-36+21`

`k=3`

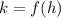
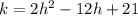
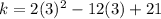
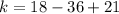
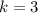
The vertex of the function is (h,k)=(3,3)

The x-coordinate of the vertex i.e.
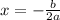`x=-(b)/(2a)` is the axis of symmetry,

So,
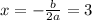`x=-(b)/(2a)=3` (solved above)

So, The axis of symmetry is x=3.