Step 1:
Write the system of equations
x - y - 2z = 4 (1)
-x + 2y + z = 1 (2)
-x + y - 3z = 11 (3)
Step 2:
From equation 1, make x subject of the relation and substitute in equation 2 to get equation 4 and equation 3 to get equation 5.
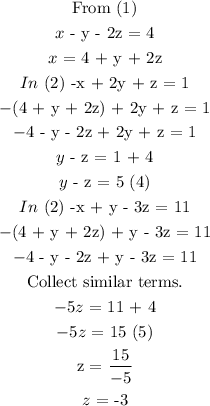
Step 3:
From equation 4, find the value of y.
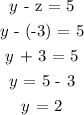
Step 4:
Substitute y and z in x = 4 + y + 2z to find the value of x.
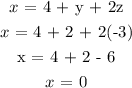
Final answer
x = 0
y = 2
z = -3