Question

A square pyramid has a height h and a base with side length b. The side lengths of the base increase by 50%. Write a simplified expression that represents the volume of the new pyramid in terms of b and h.

Answer 1

check the picture below.

now, if the width and length of the base are increased by 50%, then that means the sides are (150/100) * length and (150/100) * width, or 1.5 of each.


`\bf A=\cfrac{1}{3}Bh\quad \begin{cases} B=l\cdot w\\ l=1.5l\\ w=1.5w\\ -----\\ 1.5l\cdot 1.5w\\ 1.5(lw)\\ 1.5B \end{cases}\implies A=\cfrac{1}{3}\cdot 1.5Bh\implies A=\cfrac{1}{3}\cdot \cfrac{15}{10}Bh \\\\\\ A=\cfrac{15}{30}Bh\implies A=\cfrac{1}{2}Bh`

Answer 2

Volume of new pyramid is:

2.25bh

Explanation:

Square pyramid means a cuboid whose length and breath are equal.

Length and breath of original pyramid=b

and height=h

Volume of original pyramid=b²h

Length and breath of new pyramid=1.5b

(
`(150)/(100)* b =1.5b`)

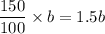and height=h

Volume of new pyramid=1.5b×1.5b×h

= 2.25bh

Hence, Volume of new pyramid is:

2.25bh