Question

If sinθ =4/5 , then cosθ = _____.

Answer 1

cosθ is 3/5 because the cosine is found from the adjacent side of the triangle being divided by the hypotenuse. The sine is found by putting the opposite side from θ over the hypotenuse. If you draw this triangle out, the side across from θ would be 4 and the hypotenuse 5. In order to find the opposite side, you could either solve with the pythagorean theorem (a^2+b^2= c^2) or you could remember the properties of a triangle, therefore the final side is 3. You then put the opposite, 3, over the hypotenuse,5, in order to get 3/5 for the cosθ.

Answer 2

cosθ =
`(3)/(5)` .

Explanation:

Given : If sinθ =4/5 .

To find : cosθ = _____.

Solution : We have given that sinθ =4/5 .

By the trigonometric identity

cos²θ + sin²θ = 1.

Plugging the value of sinθ =4/5 .

cos²θ +
`((4)/(5)) ^(2)` = 1.

cos²θ +
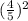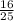`(16)/(25)` = 1.

On subtracting
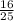`(16)/(25)` from both sides

cos²θ = 1 -
`(16)/(25)` .

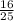cos²θ =
`(25 -16)/(25)` .

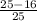Taking square root both sides.

`\sqrt{cos^(2)theta}  = \sqrt{(9)/(25)}` .

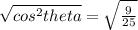cosθ =
`(3)/(5)` .

Therefore, cosθ =
`(3)/(5)` .