Question

What are the values of m x and a

Answer 1

The value of x is 3

The value of m is 5.25

The value of a is 1.75

Explanation:

I attached the picture with labels to can solve

In the 2 Δs ADE and ACF

∵ DE // CF

∴ m∠ADE = m∠ACF ⇒ corresponding angles

∴ m∠AED = m∠AFC ⇒ corresponding angles

→ By using the AA postulate of similarity

∴ The two triangles are similar

∴ Their corresponding sides have the same ratio

∴
`(AD)/(AC)` =
`(EA)/(FA)` =
`(DE)/(CF)`

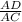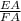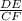
∵ AD = AB + BC + CD

∵ AB = 3, BC = 6, CD = x

∴ AD = 3 + 6 + x

∴ AD = 9 + x

∵ AC = AB + BC = 3 + 6

∴ AC = 9

∵ AE = AG + GF + FE

∵ AG = 4, GF = 8, FE = 4

∴ AE = 4 + 8 + 4

∴ AE = 16

∵ FA = AG + GF = 4 + 8

∴ FA = 12

∵ DE = 7 and CF = m

→ Substitute them in the ratio above

∴
`(9+x)/(9)` =
`(16)/(12)` =
`(7)/(m)`

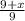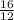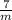
→ By using cross multiplication with the first 2 fractions

∵ 12 × (9 + x) = 9 × 16

∴ 12(9) + 12(x) = 144

∴ 108 + 12x = 144

→ Subtract 108 from both sides

∴ 108 - 108 + 12x = 144 - 108

∴ 12x = 36

→ Divide both sides by 12 to find x

∴ x = 3

→ By using cross multiplication with the second 2 fractions

∵ 16 × m = 12 × 7

∴ 16m = 84

→ Divide both sides by 16

∴ m = 5.25

In the 2 Δs ABG and ACF

∵ BG // CF

∴ m∠ABG = m∠ACF ⇒ Corresponding angles

∴ m∠AGB = m∠AFC ⇒ corresponding angles

→ By using the AA postulate of similarity

∴ The two triangles are similar

∴ Their corresponding sides have the same ratio

∴
`(AB)/(AC)` =
`(GA)/(FA)` =
`(BG)/(CF)`

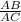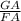∵ AB = 3 and AC = 9

∵ GA = 4 and FA = 12

∵ BG = a and CF = m = 5.25

→ Substitute them in the ratio above

∴
`(3)/(6)` =
`(4)/(12)` =
`(a)/(5.25)`

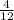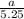
→ By using cross multiplication with the second 2 fractions

∵ 12 × a = 4 × 5.25

∴ 12a = 21

→ Divide both sides by 12 to find a

∴ a = 1.75