Question

Mr. and Mrs. Patton and their daughter Carolyn own three cars. Carolyn drives 10 miles per week farther with her car than her father does with his. Mr. Patton does twice as many miles per week as Mrs. Patton. If their total mileage per week is 160 miles, how many miles per week does each drive?

Answer 1

x = mr. pattons miles, y = mrs. patton's miles, z = carolyn's miles

x + y + z = 160
z = x + 10 ......z = 2y + 10
x = 2y

2y + y + 2y + 10 = 160
5y + 10 = 160
5y = 160 - 10
5y = 150
y = 150/5
y = 30 <=== mrs. patton drives 30 miles

x = 2y
x = 2(30)
x = 60....mr. patton drives 60 miles

z = x + 10
z = 60 + 10
z = 70 <== carolyn drives 70 miles

Answer 2

Answer: They drive 60 miles, 70 miles, 30 miles respectively.

Explanation:

Since we have given that

Total mileage per week = 160 miles

Let the number of miles that her father does be x

Let the number of miles that she does be x+10

let the number of miles that her mother does be
`(x)/(2)`

so, our equation becomes,

`x+x+10+(x)/(2)=160\\\\2x+\frac{x}2}=160-10\\\\(4x+x)/(2)=150\\\\(5x)/(2)=150\\\\x=(150* 2)/(5)\\\\x=60\ miles`

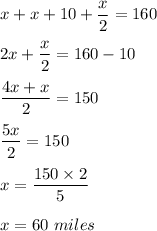
So, her father drives 60 miles.

She drives 60 +10 = 70 miles.

Her mother drives
`(60)/(2)=30\ miles`

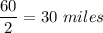
Hence, they drive 60 miles, 70 miles, 30 miles respectively.