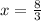Answer:
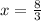 is the solution to
is the solution to
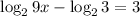
Explanation:
Using the logarithmic rules:
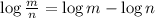
if
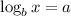 then;
then;
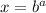
Given the equation:
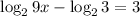
Solve for x:
Apply the logarithmic rules:
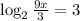
⇒
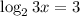
Apply the logarithmic rules;
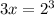
⇒

Divide both sides by 3 we have;
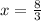
Therefore, the solution for the given equations is,