Question

Given the function f(x) = x ^ 3 - 2 and g(x) = 1/2 * x ^ 3 + 3 , which describes the transformations applied to the function f(x) so it falls onto g(x) ?

Answer 1

Option 3: The graph of g(x) has a vertical shrink by a factor of 1/2 and a vertical shift up by 5 units from the function of f(x).

Explanation:

Given the function f(x) where:

`f(x)=x^3-2`

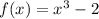
We want to determine the transformations applied on f(x) so that it falls onto g(x) where:

`g(x)=(1)/(2)x^3+3`

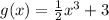
Step 1: Since the product of x³ i.e. 1/2 is less than one, f(x) has been vertically shrunk by a factor of 1/2 to obtain:

`(1)/(2)x^3-2`

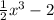
Step 2: If the result is vertically shifted up by 5 units, then:

`(1)/(2)x^3-2+5=(1)/(2)x^3+3=g(x)`

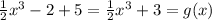
Thus, the graph of g(x) has a vertical shrink by a factor of 1/2 and a vertical shift up by 5 units from the function of f(x).

The third option is correct.