Question

Solve the following system of linear equations by substitution and determine whether the system has one solution,no solution, or an infinite number of solutions. If the system has one solution, find the solution. 3y = 9x - 30-3x + y = -10

Answer 1

Given:

`\begin{gathered} 3y=9x-30\ldots\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(1) \\ -3x+y=-10\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(2) \end{gathered}`

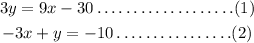
To solve using the substitution method, we make one unknown in one of the equations the subject of the formula and substitute it into the other equation.

From the given equations, make y the subject of the formula in equation (2);

`\begin{gathered} -3x+y=-10 \\ y=3x-10 \end{gathered}`

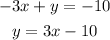
Substituting y into equation (1);

`\begin{gathered} 3y=9x-30 \\ 3(3x-10)=9x-30 \\ 9x-30=9x-30 \\ 9x-9x=-30+30 \\ 0=0 \end{gathered}`

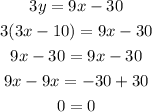
The solution shows the system has an infinite number of solutions.