Question

A satellite camera takes arectangle-shaped picture. The smallest region that can bephotographed is a 5-km by 7-km rectangle. As the camerazooms out, the length 1 and width w of the rectangle increase at a rate of 2 km/sec. How long does it take for the area A to be at least 5 times its original size?

Answer 1

Area of the smallest region that can be photographed

Area which is 5 times its original size

If the length and width increases at a rate of 2km/sec, its area at any time t (where t is in seconds) will be:

`Area=(5+2t)(7+2t)`

Now, the time it takes for the area A to be at least 5 times its original size will be the time t when:

`(5+2t)(7+2t)=175`

Next, we solve the equation derived above for t

`\begin{gathered} \implies35+10t+14t+4t^2=175 \\ \implies4t^2+24t+35-175=0 \\ \implies4t^2+24t-140=0 \\ \implies4(t^2+6t-35)=0 \\ \text{Divide both sides by 4} \\ \implies t^2+6t-35=0 \end{gathered}`

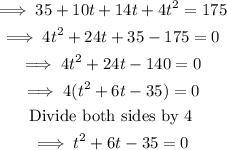
We can then solve for t using the quadratic formula

`x=(-b\pm√(b^2-4ac))/(2a)`
`\begin{gathered} t=(-6\pm√(6^2-4*1*-35))/(2*1) \\ =(-6\pm√(36+140))/(2) \\ =(-6\pm√(176))/(2) \\ =(-6\pm13.27)/(2) \\ \text{Therefore:} \\ t=(-6+13.27)/(2)\text{ or }(-6-13.27)/(2) \\ t=3.64\text{ seconds or -9.64 seconds} \end{gathered}`

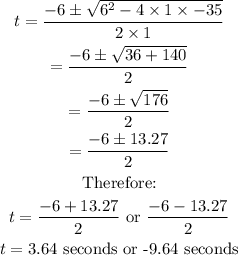
Since time cannot be a negative value, the value t=-9.64 seconds is invalid.

Therefore: t=3.64 seconds

Therefore, it would take at least 3.64 seconds for the area, A to be at least 5 times its original size.