Question

AB=3xBC=10AC=4x+1X=AB=AC=

Answer 1

We can represent the given information in a line segment for reference as shown in the following image:

Since AB=3x

And BC=10

And AC=4x+1

As we can see the sum of AB and BC (3x and 10) gives AC as the result.

So we will have an equation in which the addition of 3x+10 is equal to 4x+1:

`3x+10=4x+1`

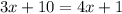
Now we need to solve this equation for x.

Subtract 3x to both sides:

`\begin{gathered} 3x-3x+10=4x-3x+1 \\ 10=4x-3x+1 \end{gathered}`

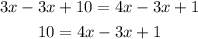
Combine like terms on the right side:

`10=x+1`

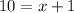
And subtract 1 to both sides:

`\begin{gathered} 10-1=x+1-1 \\ 9=x \end{gathered}`

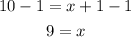
The value of x is 9.

Using that value, we find AB:

`\begin{gathered} AB=3x \\ \text{substituting x=9} \\ AB=3(9) \\ AB=27 \end{gathered}`

And we do the same to find AC:

`\begin{gathered} AC=4x+1 \\ \text{substituting x=9} \\ AC=4(9)+1 \\ AC=36+1 \\ AC=37 \end{gathered}`

Answer:

x=9

AB=27

AC=37