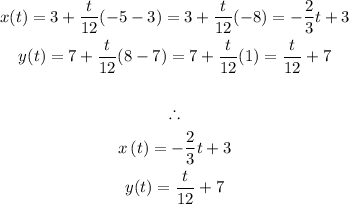Question

Hi! I need help with two problems having to do with Parametric equations.pre calculus

Answer 1

Let a and b be two-dimensional vectors. Notice that a and b can also be regarded as points in a 2D coordinate plane.

The parametric equation of a line segment that goes from a to b using a parameter t that ranges from 0 to 1 is:

`r(t)=a+t(b-a)`

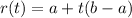
And each component would be given by:

`\begin{gathered} x(t)=x_a+t(x_b-x_a)\quad,\quad0\leq t\leq1 \\ y\left(t\right)=y_a+t\lparen y_b-y_a)\quad,\quad0\leq t\leq1 \end{gathered}`

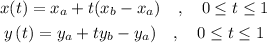
We can use an alternative parameter that moves from 0 to k replacing t for t/k:

`\begin{gathered} x\left(t\right)=x_a+(t)/(k)\left(x_b-x_a\right)\quad,\quad0\leq t\leq k \\ \\ y\left(t\right)=y_a+(t)/(k)\left(y_b-y_a\right)\quad,\quad0\leq t\leq k \end{gathered}`

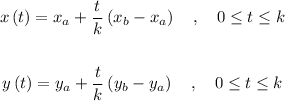
Use these expressions to find parametric equations for a line segment that connects the given points.

3) Init: (-5,8), term: (3,7)

For 0≤t≤4:

`\begin{gathered} x(t)=-5+(t)/(4)(3--5)=-5+(t)/(4)(3+5)=-5+(t)/(4)(8)=2t-5 \\ y(t)=8+(t)/(4)(7-8)=8+(t)/(4)(-1)=-(t)/(4)+8 \\ \\ \therefore \\ x\left(t\right)=2t-5 \\ y(t)=-(t)/(4)+8 \end{gathered}`

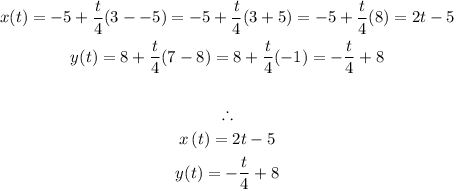
For 0≤t≤12:

`\begin{gathered} x(t)=-5+(t)/(12)(3--5)=-5+(t)/(12)(3+5)=-5+(t)/(12)(8)=(2)/(3)t-5 \\ y(t)=8+(t)/(12)(7-8)=8+(t)/(12)(-1)=-(t)/(12)+8 \\ \\ \therefore \\ x\left(t\right)=(2)/(3)t-5 \\ y(t)=-(t)/(12)+8 \end{gathered}`

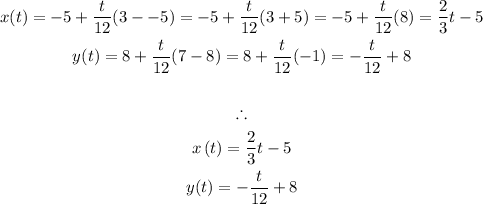
4) Init: (3,7), term: (-5,8)

For 0≤t≤4:

`\begin{gathered} x(t)=3+(t)/(4)(-5-3)=3+(t)/(4)(-8)=-2t+3 \\ y(t)=7+(t)/(4)(8-7)=7+(t)/(4)(1)=(t)/(4)+7 \\ \\ \therefore \\ x\left(t\right)=-2t+3 \\ y(t)=(t)/(4)+7 \end{gathered}`

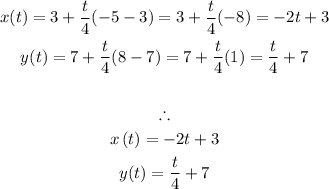
For 0≤t≤12:

`\begin{gathered} x(t)=3+(t)/(12)(-5-3)=3+(t)/(12)(-8)=-(2)/(3)t+3 \\ y(t)=7+(t)/(12)(8-7)=7+(t)/(12)(1)=(t)/(12)+7 \\ \\ \therefore \\ x\left(t\right)=-(2)/(3)t+3 \\ y(t)=(t)/(12)+7 \end{gathered}`