Substitute V = 72 into the volume formula:
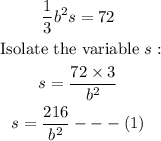
Substitute equation 1 into the Surface area formula:
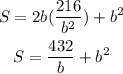
Draw the graph of the function S:
Notice that the S is minimized at b = 6.
Substitute b = 6 into equation 1:
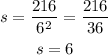
Therefore, the correct answer is choice C:
b = 6 in. and s = 6 in.