To simplify the logarithmic expression, we need to remember some logarithm rules. Some of the rules are:
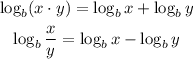
In the expression that we have, we can group it into (log₃ 54 + log₃ 10) - log₃ 20.
We can apply the logarithm product rule in this expression: log₃ 54 + log₃ 10. This becomes log₃ (54 x 10) = log₃ 540
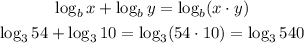
Then, we can apply the logarithm quotient rule in this expression log₃ 540 - log₃ 20. This becomes log₃ (540/20) = log₃ 27 which is equal to 3.
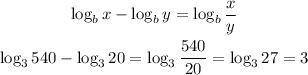
The single logarithm is:

which then simplified to:
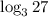
which is equal to 3.