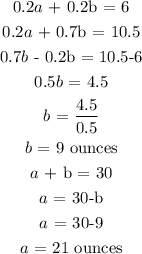Question

Solve this percent mixture problem using a system of linear equations A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 20% salt and Solution B is 70% salt. She wants to obtain 30 ounces of a mixture that is 35% salt. How many ounces of each solution should she use? Solution A=(. )Ounces Solution B=(. )Ounces

Answer 1

`\begin{gathered} \text{Solution A = 21 ounces} \\ \text{Solution B = 9 ounces} \end{gathered}`

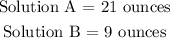
Step-by-step explanation:

Let the number of ounces of solution A be a

Let the number of ounces of solution B be b

The sum total of the ounces is 30

Thus:

`a\text{ + b = 30}`

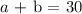
Now, let us work with the percentages

Mathematically, we have it that:

`\begin{gathered} 20\text{ \% salt solution A + 70\% salt solution B = 35 \% salt total} \\ 0.2(a)\text{ + 0.7(b) = 0.35(30)} \\ 0.2a\text{ + 0.7b = 10.5} \end{gathered}`

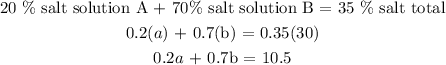
The two linear equations we are to solve simultaneously are:

`\begin{gathered} a\text{ + b = 30} \\ 0.2a\text{ + 0.7b = 10.5} \end{gathered}`

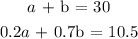
Multiply equation 1 by 0.2 and equation 2 by 1: we have:

`\begin{gathered} 0.2a\text{ + 0.2b = 6} \\ 0.2a\text{ + 0.7b = 10.5} \\ 0.7b\text{ - 0.2b = 10.5-6} \\ 0.5b\text{ = 4.5} \\ b\text{ = }(4.5)/(0.5) \\ b\text{ = 9 ounces} \\ a\text{ + b = 30} \\ a\text{ = 30-b} \\ a\text{ = 30-9} \\ a\text{ = 21 ounces} \end{gathered}`