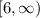Question

Solve the following inequalities. write the final solutions i. intreval botation

Answer 1

Step 1. The inequality we have is:

`2-3x\ge7(8-2x)+12`

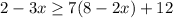
And we are asked to find the solution in interval notation.

The first step will be to apply the distributive property on the right-hand side of the inequality to solve the expression 7(8-2x). The distributive property tells us to multiply 7 by 8 and also 7 by -2, the resulting expression is:

`2-3x\ge56-14x+12`

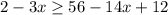
here, 56 comes from 7*8, and -14x comes from multiplying 7 times -2x.

Step 2. The next step will be to have all of the terms containing x on one side of the inequality. For this, we add 14x to both sides of the inequality:

`2-3x+14x\ge56-14x+14x+12`

On the left-hand side -3x+14x is equal to 11x:

`2+11x\ge56-14x+14x+12`

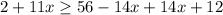
and on the right-hand side, -14x+14x cancel each other:

`2+11x\ge56+12`

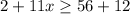
Step 3. The next step is to add the like terms on the right-hand side:

`2+11x\ge68`

And in order to leave the term 11x alone on the left side of the inequality, we subtract 2 to both sides:

`\begin{gathered} 2-2+11x\ge68-2 \\ 11x\ge66 \end{gathered}`

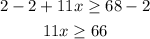
Step 4. To solve for x, divide both sides by 11:

`\begin{gathered} (11x)/(11)\ge(66)/(11) \\ \end{gathered}`

the result is:

`x\ge6`

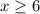
Step 5. Since the result is that x is greater or equal to 6, in interval notation we will have the following expression to represent this result:

`\lbrack6,\infty)`

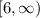
This means that the final solutions are the numbers going from 6 to infinity.

Answer:

`\lbrack6,\infty)`