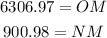Question

Need to find OM and NM given AO= 6371 angle NOE= 16.26 deg and that AO bisects angle NOEIf it helps at all the point O is in the center of the circle and segment OA is the radius

Answer 1

As you can see the segments OM ME and OE form a right triangle. So to find the measure of the segment OM you can use the trigonometric ratio cos (θ):

`\cos (\theta)=\frac{\text{ Adjacent side}}{\text{ Hypotenuse}}`

So, you have:

`\begin{gathered} \cos (MOE\text{)}=(OM)/(OE) \\ \cos (8.13\text{\degree)}=(OM)/(6371) \end{gathered}`

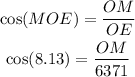
Angle MOE measures 8.13 ° because segment AO bisects angle NOE.

`\frac{16.26\text{\degree}}{2}=8.13\text{\degree}`

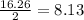
The measure of segment OE is 6371 because it is a radius of the circle just like segment AO.

`\begin{gathered} \cos (8.13\text{\degree)}=(OM)/(6371) \\ \text{ Multiply by 6371 on both sides of the equation } \\ \cos (8.13\text{\degree)}\cdot6371=(OM)/(6371)\cdot6371 \\ \cos (8.13\text{\degree)}\cdot6371=OM \\ 6306.97=OM \end{gathered}`

Now, to find the measure of segment NM you can use the trigonometric ratio sin (θ):

`\sin (\theta)=\frac{\text{Opposite side}}{\text{ Hypotenuse}}`

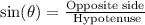
Also, the NM and ME segments are equal because the AO segment bisects the NOE angle. So, you have:

`NM=ME`
`\begin{gathered} \sin (MOE)=(ME)/(OE) \\ \sin (8.13\text{\degree})=(ME)/(6371) \\ \text{ Multiply by 6371 on both sides of the equation} \\ \sin (8.13\text{\degree})\cdot6371=(ME)/(6371)\cdot6371 \\ \sin (8.13\text{\degree})\cdot6371=ME \\ 900.98=ME \\ \text{ Then} \\ 900.98=NM \end{gathered}`

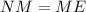
Therefore, the measurements of the OM and NM segments are:

`\begin{gathered} 6306.97=OM \\ 900.98=NM \end{gathered}`