Question

The sum of the base and height of a triangle is 12 cm. What is the largest area that the triangle can have?(detialed answer)

Answer 1

Given:

The sum of the base and height of a triangle is 12cm.

To find:

The largest possible area of the triangle.

Step-by-step explanation:

According to the problem,

`\begin{gathered} x+h=12........(1) \\ x=12-h........(2) \end{gathered}`

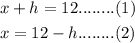
Using the area formula of the triangle,

`\begin{gathered} A=(1)/(2)bh \\ A=(1)/(2)x\cdot h.........(3) \end{gathered}`

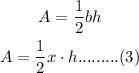
Substituting equation (2) in (3),

`\begin{gathered} A(h)=(1)/(2)(12-h)h \\ A(h)=6h-(h^2)/(2)..........(4) \end{gathered}`

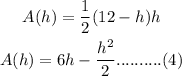
Using the first derivative test,

`\begin{gathered} A^(\prime)(h)=0 \\ 6-(2h)/(2)=0 \\ 6-h=0 \\ -h=-6 \\ h=6 \end{gathered}`

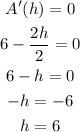
Since,

`A^(\prime)^(\prime)(h)=-2<0`

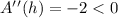
So, it has a maximum value of h = 6.

Substituting h = 6 in equation (2) we get,

`\begin{gathered} x=12-6 \\ x=6 \end{gathered}`

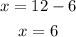
Therefore, the largest possible area will be,

`\begin{gathered} A=(1)/(2)bh \\ =(1)/(2)*6*6 \\ =18cm^2 \end{gathered}`

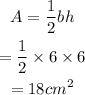
Final answer:

The largest possible area of the triangle is 18 square cm.