Given:
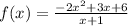
Required:
We need to find the horizontal or oblique asymptote of f(x).
Step-by-step explanation:
The degree of the numerator is 2.
The degree of the denominator is 1.
The polynomial in the numerator is a higher degree than the polynomial in the denominator.
Recall that a slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.
To find the slant asymptote you must divide the numerator by the denominator using either long division or synthetic division.
Use the long division method.
We don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line.
The slant asymptote is
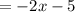
To find the horizontal asymptote divide the leading coefficient of the numerator by the leading coefficient of the denominator.
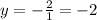
The horizontal asymptote is
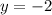
Final answer: