Question

Tutorial Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. Gymnasts training for an upcoming competition are practicing their routines for balance beam and floor exercise. During morning practice, Rosanne practiced her beam routine 1 time and her floor routine 1 time, which took a total of 3 minutes. During afternoon practice, she ran through her her beam routine 4 times and her floor routine 6 times, which took a total of 14 minutes. How long is each routine? The beam routine is minutes long and the floor exercise is minutes long.

Answer 1

Given that:

- In the morning, Rosanne practiced her beam routine 1 time and her floor routine 1 time, which took a total of 3 minutes.

- In the afternoon, Rosanne praticed her beam routine 4 times and her floor routine 6 times, which took a total of 14 minutes.

Let be "b" the length (in minutes) of the beam routine and "f" the length (in minutes) of the floor exercise.

Using the data given in the exercise, you can set up this System of Equations:

`\begin{cases}b+f={3} \\ 4b+6f={14}\end{cases}`

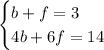
Where the first equation represents the length (in minutes) of Rossane's routine in the morning, and the second equation represents the length (in minutes) of her routine in the afternoon.

You can solve the System of Equations using the Elimination Method as follows:

1. Multiply the first equation by -4:

`\begin{cases}-4b-4f={-12} \\ 4b+6f={14}\end{cases}`

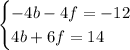
2. Add the equations:

`\begin{gathered} \begin{cases}-4b-4f={-12} \\ 4b+6f={14}\end{cases} \\ --------- \\ 0b+2f=2 \\ 2f=2 \end{gathered}`

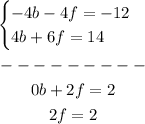
3. Solve for "f":

`\begin{gathered} f=(2)/(2) \\ \\ f=1 \end{gathered}`

4. Substitute the value of "f" into the first original equation and solve for "b":

`\begin{gathered} b+(1)=3 \\ b=3-1 \\ b=2 \end{gathered}`

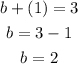
Hence, the answer is: The beam routine is 2 minutes long and the floor exercise is 1 minute long.