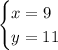By definition, a parallelogram is a quadrilateral with opposite sides parallel and equal.
Since the opposite sides are equal, the following equations are true

Solving the first equation, we have

Solving the second equation, we have
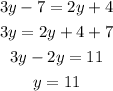
And those are the solutions.