Question

In order to estimate the length of the runway, a passenger on an airplane jotted down some velocity data during takeoff fromthe on-board entertainment screen. From the resulting table given below, calculateto find his estimate. Round any intermediate calculations, if needed, to no less than six decimal places, and round your final answer to three decimal places.

Answer 1

We are given a table with values of time and velocity and we are asked to determine the distance. To do that we need to have into account that the distance is the area under the curve of a time vs velocity table. First, the graph of the points is the following:

Here we have divided the area under the curve into 7 rectangles using the smallest value of velocity for each interval of 6 seconds. The 6 second interval is the base of the rectangle. To determine the total area under the curve we need to add the areas of each of the rectangles. Doing that we get:

`U_8=(20(miles)/(h))(6s)+(79(miles)/(h))(6s)+(110(miles)/(h))(6s)+(150(miles)/(h))(6s)+(170(miles)/(h))(6s)+(204(miles)/(h))(6s)+(223(miles)/(h))(6s)`

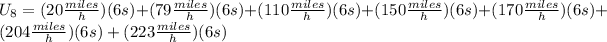
We also notice that each rectangle lies under the curve. Solving the operations we get:

`U_8=5736`

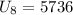
Now, if we take the largest value of velocity for each interval we get:

Now the rectangles are over the curve. The area is the sum of the areas of each rectangle, therefore, we have:

`O_8=(79)(6)+(110)(6)+(150)(6)+(170)(6)+(204)(6)+(223)(6)+(230)(6)`

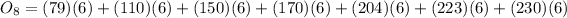
Solving the operations we get:

`O_8=6996`

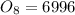
Now we apply the formula:

`d=(O_8+U_8)/(2)`

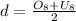
Substituting the values:

`d=(6996+5736)/(2)=6366`

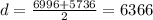
Therefore, the distance is 6366 miles.