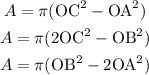Question

I need help with a geometry. I have attached the assignment I need help with

Answer 1

1)

The smallest circle has a radius of 3 (the segment OA is 3), we can use the area formula to solve it

`A=\pi r^2`

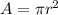
Here the radius is 3, therefore the area is

`\begin{gathered} A=\pi r^2 \\ \\ A=\pi(3)^2 \\ \\ A=9\pi \end{gathered}`

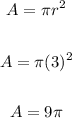
The area of the smallest circle is 9π, it's approximately 28.2743.

2)

The area of the yellow ring will be the area of the outer circle minus the area of the middle circle. We know that the radius of the outer circle is the segment OB, the diagonal of the rectangle, and the radius of the middle circle is OC, therefore the area of the ring is

`\begin{gathered} A=\pi\text{OB}^2-\pi\text{OC}^2 \\ \\ A=\pi(\text{OB}^2-\text{OC}^2) \end{gathered}`

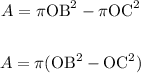
But we can write OB, the diagonal of the rectangle, using OC and OA, to do that we must use Pythagoras, and we can say that

`\text{OB}^2=\text{OA}^2+\text{OC}^2`

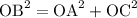
Now let's use that result in the area formula we got

`\begin{gathered} A=\pi(\text{OB}^2-\text{OC}^2) \\ \\ A=\pi(\text{OA}^2+\text{OC}^2-\text{OC}^2) \\ \\ A=\pi\text{OA}^2 \end{gathered}`

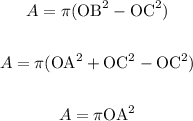
And we have this very interesting result, the area of the yellow ring is equal to the area of the smallest circle!

3)

The area of the white ring would be similar, now we have the area of the middle circle minus the inner circle, therefore

`A=\pi(\text{OC}^2-\text{OA}^2)`

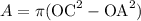
We can keep this formula or we can write other variations too, see that

`\text{OB}^2=\text{OA}^2+\text{OC}^2\Rightarrow\text{OA}^2=\text{OB}^2-\text{OC}^2`

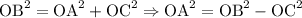
Then

`\begin{gathered} A=\pi(\text{OC}^2-\text{OA}^2) \\ \\ A=\pi(\text{OC}^2-(\text{OB}^2-\text{OC}^2)) \\ \\ A=\pi(2\text{OC}^2-\text{OB}^2) \end{gathered}`

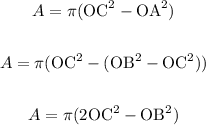
Or

`\text{OB}^2=\text{OA}^2+\text{OC}^2\Rightarrow\text{OC}^2=\text{OB}^2-\text{OA}^2`

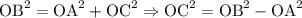
Then

`\begin{gathered} A=\pi(\text{OC}^2-\text{OA}^2) \\ \\ A=\pi(\text{OB}^2-\text{OA}^2-\text{OA}^2) \\ \\ A=\pi(\text{OB}^2-2\text{OA}^2) \end{gathered}`

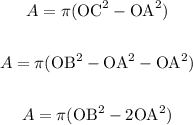
The three possibilities for the white ring is

`\begin{gathered} A=\pi(\text{OC}^2-\text{OA}^2) \\ A=\pi(2\text{OC}^2-\text{OB}^2) \\ A=\pi(\text{OB}^2-2\text{OA}^2) \end{gathered}`