Question

A passenger jet passed through an altitude of 13,000 feet 8 minutes after takeoff and was climbing at a rate of 1,250 feet per minute. Find a linear model for the altitude A (in ft) of the jet t minutes after takeoff.A = __________Use your model to predict the altitude (in ft) of the jet 12 minutes into the flight._________ ft

Answer 1

A represents the altitude in feet.

t represents the minutes after takeoff

You have to create a linear model for the altitude with respect to the time:

`A=mt+b`

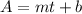
m → slope

b→ y-intercept

You know that the jet increased its altitude at a rate of 1250ft/min, this value represents the slope of the linear model.

You can express it as follows:

`A=1250t+b`

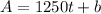
After 8 minutes the jet had an altitude of 13000ft, using these values you can determine the y-intercept of the linear model, replace them in the expression:

`\begin{gathered} A=1250t+b \\ 13000=1250\cdot8+b \end{gathered}`

Solve for b

`\begin{gathered} 13000=1250\cdot8+b \\ 13000=10000+b \\ 13000-10000=1000-10000+b \\ 3000=b \end{gathered}`

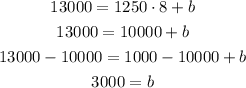
The y-intercept of the model is 3000ft

So the model for the altitude of the yet is

`A=1250t+3000`

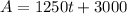
To predict the altitude after 12 minutes you have to replace the model with t=12 and solve for A:

`\begin{gathered} A=1250\cdot12+3000 \\ A=15000+3000 \\ A=18000ft \end{gathered}`

The altitude of the jet after 12 minutes is 18,000ft