Question

Reflect (-3,1) over the y-axis.Then translate the result to the right 1 unit. What are the coordinates of the final point?

Answer 1

A reflection is a transformation representing a flip of a figure. Figures may be reflected in a point, a line, or a plane. When reflecting a figure in a line or in a point, the image is congruent to the preimage.

A reflection maps every point of a figure to an image across a fixed-line. The fixed line is called the line of reflection.

There are different reflections but the one under consideration is a reflection over the y-axis. The reflection rule over the y-axis is given as

`(x,y)\rightarrow(-x,y)`

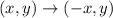
Given the coordinate (-3, 1). The reflection over the y-axis of the point given is

`\begin{gathered} (-3,1)\rightarrow(--3,1) \\ =(-3,1)\rightarrow(3,1) \end{gathered}`

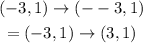
In a translation transformation, all the points in the object are moved in a straight line in the same direction. The size, shape, and orientation of the image are the same as that of the original object. The same orientation means that the object and image are facing the same direction.

We describe a translation in terms of the number of units moved to the right or left and the number of units moved up or down.

Given that the point is then translated by moving to the right by 1 unit. The translation rule for moving to the right is given as

`\begin{gathered} (x,y)\rightarrow(x+a,y) \\ \text{where is number of unit} \end{gathered}`

Since our new result is the point (3, 1). Then the translation would give

`\begin{gathered} (3,1)\rightarrow(3+a,y) \\ \text{when a = 1, then} \\ (3,1)\rightarrow(3+1,1) \\ =(3,1)\rightarrow(4,1) \end{gathered}`

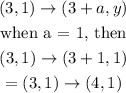
Hence, the coordinates of the final point is (4, 1)