Question

Use a graph to predict when the population will fall below 8,000

Answer 1

An exponential function has the form:

`y=A(r)^x`

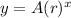
Where A is the initial value, r is the ratio that is applied for each period of time and x is the time since the initial A in the same unit as the period of r.

The initial value of the population was 15500, so:

`A=15500`

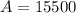
It decreases 3% per year, so x is the time since the population was 15500 in years and, since it is a 3% decrease, this means that after each year there are just 97% left, so the ratio is 97% or, in the decimal form, 0.97.

`\begin{gathered} x\Longrightarrow\; \text{time in years since the initial population of 15500} \\ r=0.97 \end{gathered}`

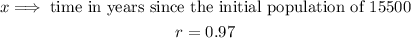
So, the function is:

`y=15500(0.97\text{)}^x`

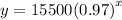
To graph the function, we can first plot some points.

Let's plot one point per 10 year until we pass the value of 8000.

For x = 0:

`y=15500(0.97)^0=15500\cdot1=15500`

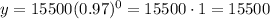
For x = 10:

`y=15500(0.97)^(10)=15500\cdot0.737424\ldots\approx11.430`

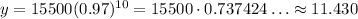
For x = 20:

`y=15500(0.97)^(20)=15500\cdot0.543794\approx8429`

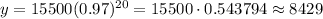
Now that we are close, let's do 2 years:

For x = 22:

`y=15500(0.97)^(22)=15500\cdot0.511656\ldots\approx7931`

So, ploting the points and graphing, we have:

The dotted line is the y = 8000. We can see that in the 21th year, the population is still above 8000, but at year 22 the population went belowe 8000.

So, the population will drop below 8000 by the 22th year since the initial population of 15500.