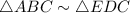Answer: 'Triangle ABC is similar to triangle EDC , because
 and
and
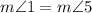
' is the correct option.
Step-by-step explanation:
Since, Here
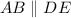 and BD and AE are the transversals which cut these two parallel lines
and BD and AE are the transversals which cut these two parallel lines
Thus according to the figure,
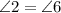 ( Because alternative interior angles made by the same transversal on two parallel lines are always equal)
( Because alternative interior angles made by the same transversal on two parallel lines are always equal)
Similarly,
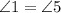
Thus In triangles ABC and DCE,
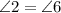
And,
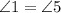
thus If In two triangles two corresponding angles are equal, then they are similar to each other.
Therefore,