Question

In a certain town, 30% of the people own dogs. (So the probability of a person being a dog-owner is 30%).

Answer 1

From the question,

We are given that the probability of a person being a dog-owner is 30%

Therefore,

The probability of a person not being a dog-owner is 70%

Hence

probability of success, p= 30%

Probability of failure, q = 70%

By binomial probability formula we have

`p(x)=^nC_xp^{x^{}}q^(n-x)`

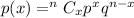
Part A

We are to find the probability of exactly 4 dog-owners if 10 dog owners are randomly selected

This implies

x = 4, n = 10

Applying the formula

`\begin{gathered} p(4)=^(10)C_4(0.3)^4(0.7)^(10-4) \\ P(4)=210*(81)/(10000)*0.1176 \\ p(4)=0.2 \end{gathered}`

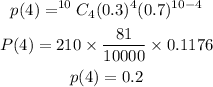
Therefore, the probability that exactly 4 own dogs is 0.2

Part B

We are to find the probability that at least 4 of them own dogs

at least 4 means 4 and above

Therefore

The probability of at least 4 will be

`\begin{gathered} p(x\ge4)=1-p(x<4) \\ p(x\ge4)=1-\lbrack(p(x=0)+p(x=1)+p(x=2)+p(x=3)\rbrack \end{gathered}`

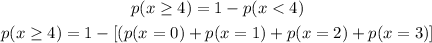
By substituting values we have

`p(x\ge4)=1-\lbrack^(10)C_0p^0q^(10)+^(10)C_1p^1q^9+^(10)C_2p^2q^8+^(10)C_3p^3q^7\rbrack`

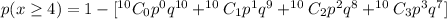
Hence, we have

`\begin{gathered} p(x\ge4)=1-\lbrack1*1*0.028^{}+10*0.3*0.04+45*0.09*0.057+120*0.027*0.082\rbrack \\ p(x\ge4)=1-\lbrack0.028+0.12+0.231+0.266\rbrack \\ p(x\ge4)=1-0.645 \\ p(x\ge4)=0.355 \end{gathered}`

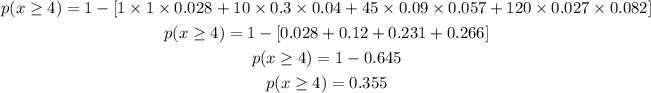
Therefore, the probability that at least 4 of them own dogs is 0.355